now to comments to your comments:
On 12.01.2016 18:43, Jason Matusiak
wrote:
Exactly what I had in mind.Thanks for the quick response Marcus!!!! Since my Latex isn't very good (as in pretty much non-existent). Let me see if I can rewrite what you recommended in my dumbed down language and see if I am close.: *I have two dongles, dongle 1 will be my modified dongle, dongle 2 will be my un-modified dongle. *Put a a known reference tone into each of the dongles where Ftune = Fref - Foffset ** Foffset should be roughly a third of the sample rate
Yep.**An example at a sample rate of 1.024Msps would be a reference tone at 98MHz, and then tune the dongles to 97.659MHz *I'll now see a baseband signal for both dongles whose offsets won't be exactly the same.
For close being identical , yes :)*Multiple the resulting signals found above against each other (offset,1 * offset,2) *Pass that through a LPF with a cutoff of Fsample/4, or 256khZ in this case **This will give the difference between the frequencies at frequency at Foffset,1 +/- Foffset,2 *perform a QT freq sync or a quad demod into a QT time sink to compare. Is that close?
That's modulation. So, the math behind that is:I think I am missing something in there, and I have a feeling that it has to do with the multiplication step as that makes the least amount of sense to me. Any way to enlighten me on what I am missing above? Thanks!
Let's consider both tones to be cosines. Thanks to Euler, we know we can express a cosine as (
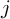is the
imaginary unit, 
)
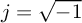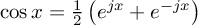; therefore, 
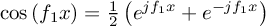. Now,
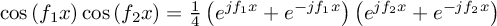.Let's expand the multiplication of the two (), and use the fact that
:![\documentclass{article}
\usepackage[utf8x]{inputenc}
\usepackage{amsmath}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage[usenames,dvipsnames]{xcolor}
\usepackage{trfsigns}
\DeclareMathOperator*{\argmin}{arg\,min}
\usepackage{tikz}
\usepackage{circuitikz}
\usepackage[binary-units=true]{siunitx}
\sisetup{exponent-product = \cdot}
\DeclareSIUnit{\dBm}{dBm}
\newcommand{\imp}{\SI{50}{\ohm}}
\newcommand{\wrongimp}{\SI{75}{\ohm}}
\pagestyle{empty}
\begin{document}
\begin{align*}
e^{j f_1 x}e^{j f_2 x}&+e^{j f_1 x}e^{-j f_2 x}&+ e^{-j
f_1 x}e^{j f_2 x}&+ e^{-j f_1 x}e^{-j f_1 x}\\
=e^{j f_1 x+j f_2 x}&+e^{j f_1 x-j f_2 x}&+ e^{-j f_1 x+j
f_2 x}&+ e^{-j f_1 x+-j f_2 x}\\
= e^{j ( f_1 +f_2)x}&+e^{j( f_1 - f_2)x}&+ e^{j( -f_1+
f_2)x}&+ e^{j(- f_1 - f_2)x}\\
= {\color{blue}e^{j ( f_1 +f_2)x}}&+{\color{OliveGreen}e^{j(
f_1 - f_2)x}}&+{\color{OliveGreen} e^{-j( f_1- f_2)x}}&+
{\color{blue} e^{-j( f_1 + f_2)x}}\\
\end{align*}
\end{document}](pngqxmfMyeR4X.png "\documentclass{article}
\usepackage[utf8x]{inputenc}
\usepackage{amsmath}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage[usenames,dvipsnames]{xcolor}
\usepackage{trfsigns}
\DeclareMathOperator*{\argmin}{arg\,min}
\usepackage{tikz}
\usepackage{circuitikz}
\usepackage[binary-units=true]{siunitx}
\sisetup{exponent-product = \cdot}
\DeclareSIUnit{\dBm}{dBm}
\newcommand{\imp}{\SI{50}{\ohm}}
\newcommand{\wrongimp}{\SI{75}{\ohm}}
\pagestyle{empty}
\begin{document}
\begin{align*}
e^{j f_1 x}e^{j f_2 x}&+e^{j f_1 x}e^{-j f_2 x}&+ e^{-j
f_1 x}e^{j f_2 x}&+ e^{-j f_1 x}e^{-j f_1 x}\\
=e^{j f_1 x+j f_2 x}&+e^{j f_1 x-j f_2 x}&+ e^{-j f_1 x+j
f_2 x}&+ e^{-j f_1 x+-j f_2 x}\\
= e^{j ( f_1 +f_2)x}&+e^{j( f_1 - f_2)x}&+ e^{j( -f_1+
f_2)x}&+ e^{j(- f_1 - f_2)x}\\
= {\color{blue}e^{j ( f_1 +f_2)x}}&+{\color{OliveGreen}e^{j(
f_1 - f_2)x}}&+{\color{OliveGreen} e^{-j( f_1- f_2)x}}&+
{\color{blue} e^{-j( f_1 + f_2)x}}\\
\end{align*}
\end{document}")
Now, let's sort this, and lo!
![\documentclass{article}
\usepackage[utf8x]{inputenc}
\usepackage{amsmath}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage[usenames,dvipsnames]{xcolor}
\usepackage{trfsigns}
\DeclareMathOperator*{\argmin}{arg\,min}
\usepackage{tikz}
\usepackage{circuitikz}
\usepackage[binary-units=true]{siunitx}
\sisetup{exponent-product = \cdot}
\DeclareSIUnit{\dBm}{dBm}
\newcommand{\imp}{\SI{50}{\ohm}}
\newcommand{\wrongimp}{\SI{75}{\ohm}}
\pagestyle{empty}
\begin{document}
\begin{align*}
= {\color{blue}e^{j ( f_1 +f_2)x}}+ {\color{blue} e^{-j( f_1 +
f_2)x}} &+{\color{OliveGreen}e^{j( f_1 -
f_2)x}}+{\color{OliveGreen} e^{-j( f_1- f_2)x}}\\
= \left( {\color{blue}e^{j ( f_1 +f_2)x} + e^{-j( f_1 + f_2)x}}
\right)&+\left({\color{OliveGreen}e^{j( f_1 - f_2)x} +e^{-j(
f_1- f_2)x}}\right)\\
= 2 \cos\left((f_1+f_2)x\right) &+
2\cos\left((f_1-f_2)x\right)\text.
\end{align*}
\end{document}](pngCyqhGTQsLu.png "\documentclass{article}
\usepackage[utf8x]{inputenc}
\usepackage{amsmath}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage[usenames,dvipsnames]{xcolor}
\usepackage{trfsigns}
\DeclareMathOperator*{\argmin}{arg\,min}
\usepackage{tikz}
\usepackage{circuitikz}
\usepackage[binary-units=true]{siunitx}
\sisetup{exponent-product = \cdot}
\DeclareSIUnit{\dBm}{dBm}
\newcommand{\imp}{\SI{50}{\ohm}}
\newcommand{\wrongimp}{\SI{75}{\ohm}}
\pagestyle{empty}
\begin{document}
\begin{align*}
= {\color{blue}e^{j ( f_1 +f_2)x}}+ {\color{blue} e^{-j( f_1 +
f_2)x}} &+{\color{OliveGreen}e^{j( f_1 -
f_2)x}}+{\color{OliveGreen} e^{-j( f_1- f_2)x}}\\
= \left( {\color{blue}e^{j ( f_1 +f_2)x} + e^{-j( f_1 + f_2)x}}
\right)&+\left({\color{OliveGreen}e^{j( f_1 - f_2)x} +e^{-j(
f_1- f_2)x}}\right)\\
= 2 \cos\left((f_1+f_2)x\right) &+
2\cos\left((f_1-f_2)x\right)\text.
\end{align*}
\end{document}")
Which means that
![\documentclass{article}
\usepackage[utf8x]{inputenc}
\usepackage{amsmath}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage[usenames,dvipsnames]{xcolor}
\usepackage{trfsigns}
\DeclareMathOperator*{\argmin}{arg\,min}
\usepackage{tikz}
\usepackage{circuitikz}
\usepackage[binary-units=true]{siunitx}
\sisetup{exponent-product = \cdot}
\DeclareSIUnit{\dBm}{dBm}
\newcommand{\imp}{\SI{50}{\ohm}}
\newcommand{\wrongimp}{\SI{75}{\ohm}}
\pagestyle{empty}
\begin{document}
\begin{align*}
\cos \left( f_1 x \right) \cos \left( f_2 x \right) &= \frac14
\left[ 2 \cos\left((f_1+f_2)x\right) +
2\cos\left((f_1-f_2)x\right)\right]\\
&=\frac12 \cos\left((f_1+f_2)x\right) +
\frac12\cos\left((f_1-f_2)x\right)
\end{align*}
\end{document}](pngagbDY94tCJ.png "\documentclass{article}
\usepackage[utf8x]{inputenc}
\usepackage{amsmath}
\usepackage{amsfonts}
\usepackage{amssymb}
\usepackage[usenames,dvipsnames]{xcolor}
\usepackage{trfsigns}
\DeclareMathOperator*{\argmin}{arg\,min}
\usepackage{tikz}
\usepackage{circuitikz}
\usepackage[binary-units=true]{siunitx}
\sisetup{exponent-product = \cdot}
\DeclareSIUnit{\dBm}{dBm}
\newcommand{\imp}{\SI{50}{\ohm}}
\newcommand{\wrongimp}{\SI{75}{\ohm}}
\pagestyle{empty}
\begin{document}
\begin{align*}
\cos \left( f_1 x \right) \cos \left( f_2 x \right) &= \frac14
\left[ 2 \cos\left((f_1+f_2)x\right) +
2\cos\left((f_1-f_2)x\right)\right]\\
&=\frac12 \cos\left((f_1+f_2)x\right) +
\frac12\cos\left((f_1-f_2)x\right)
\end{align*}
\end{document}")
Now you see where the low pass filter comes into play:
it filters out the
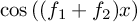component, leaving you with 
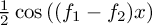, which is an oscillation with the
difference frequency.Best regards,
Marcus